Cryptoshifts
- Cryptoshifts
Cryptoshifts
Activity Highlights & Video Explanation
Highlights:
-
- Exploration of words that can be made up using shortened alphabets
-
Students apply cyphers to code different messages
- Problem solve and reason to determine constraints for cyphers which work, and those which don’t.
Video Explanation:
Pre-lesson Preparation
Prepare the investigation boards:
-
-
Download & print out 5 sets of the ‘Cyptoshifts templates’ (located at the top of the page).
-
Laminate each sheet so that students can write on them using a whiteboard marker.
-
Collect equipment:
-
- 5x laminated Cryptoshifts sets (1 set per group)
- 1x whiteboard marker and mini eraser per student.
Suggested Learning Goals & Success Criteria
| Learning Goals | Success Criteria |
|
To be able to work mathematically
|
I can:
|
| To be able to work collaboratively with peers |
I can:
|
| Apply mathematical skills when problem solving |
I can:
|
Note: You can take this task in many directions and use it to build a range of different social, cognitive, and behavioural skills within your students. The suggestions above are only a few examples of the skills which this task could be used to teach. We recommend you think about the students in your class, their specific learning needs and how this task might be used to address these when determining your learning goals and success criteria for your students.
Prerequisite Skills
This activity requires the following pre-requisit skills:
-
- Subsitution into a formula
- Students should also be reasonably confident with multiplication and division with remainders
Engage
Suggested intro:
Main Activity
Introduce the main activity:
-
- Have you ever heard the word ‘crypto’ being used before? This is where people use coded messages so that only certain people can understand what is being sent. This happens all of the time on the internet! To create these messages we can start with a word or a message and apply an encyption in order to protect what we want to say from prying eyes. Once we have encrypted our message, only those with a cypher (a mathematical key) can interpret our this message.
- For example, let’s suppose our alphabet only has 8 letters like we explored in the intro, and we wanted to encypt the message ‘cabbage head’. We might apply an encyption key of 3n, where n is the original starting position of each letter. This means that the original position of each letter gets multiplied by 3 and moves to a new position. This can be seen in the two images below:
- Image 1: Determining the position
-
Letter Starting Position Applying Key Finishing Position a 1 1*3 3rd b 2 2*3 6th c 3 3*3 9th d 4 4*3 12th e 5 5*3 15th f 6 6*3 18th g 7 7*3 21st h 8 8*3 24th - Image 2: Finding the encryption
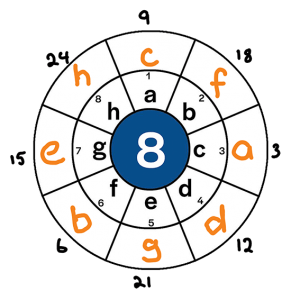
- Therefore, the following code is appied
-
Original letter Becomes a c b f c a d d e g f b g e h h - Turning the phrase ‘cabbage head’ into ‘acffceg hgcd’
- But not all encryptions will work. Take for example, an encription of 6n. This would give the following results:
- Image 3: Determining the position for 6n
-
Letter Starting Position Applying Key Finishing Position a 1 1*6 6th b 2 2*6 12th c 3 3*6 18th d 4 4*6 24th e 5 5*6 30th f 6 6*6 36th g 7 7*6 42nd h 8 8*6 48th - Image 2: Finding the encryption for 6n
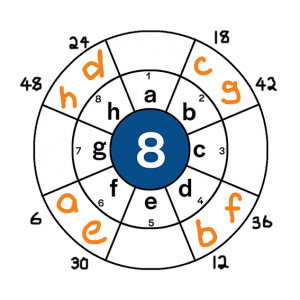
- Therefore, the following code is appied
-
Original letter Becomes a f b d c b d h e f f d g b h h - This is problematic, because we have overlapping encryptions (e.g. f now represents both a and e).
- The purpose of this task is to determine the encryptions which work, and those which don’t.
Pedagogical Recommendations:
-
- Get students exploring just the 8 letter alphabet initially. As they become confident, introduce the circles with other sized alphabets.
- Allow students to play with the probelm for a while. As you move around the room, look for students who are keeping track of their thinking by recording their work. Once students have had the opportunity to explore the task for a while, stop the class and draw everyone’s attention to the strategies that students are using to do this.
- We have found that an effective way to track students’ work is to set up a table similar to the one that can be seen below. As students explore the problem, invite them to enter their findings into the table.
Alphabet size Encryptions which work Those which don’t work 8 9 … 26 etc. - Encourage students to make conjectures and share these with the class whilst exploring the problem. Write each conjecture up on the board with the student’s name next to it to give them ownership of their thoughts.
- Celebrate all conjectures, regardless of whether or not they turn out to be correct. Every conjecture is evidence of reasoning and helps the group to progress in their thinking, irrespective of whether it turns out to be proven or disproven.
Extensions
Taking things further:
-
-
Get students to explore what happens with different types of encryptions e.g. 2n+3, n² etc.
- Get students to write a coded message to a friend using an encryption key of their choice. Once they have done this, encourage them to message to their friend, along with the key in order to decypher it.
-
Summary & Assessment
Suggested Reflection Prompt:
Get students to answer the following prompts:
Spoilers: Helpful Hints & Answers
Helpful Hints
Initially, students are likely to try a number of different cyphers with different sized alphabets. The key to identifying any patterns which emerge is to organise all of the obtained results in a way which can be read and interpreted easily. One way that we have found works is to create a table similar to the one shown below…
| Alphabet Size | Cyphers which work | Cypheres which don’t work |
| 5 | 2, 3, 4, 7, 8 etc. | 1, 5, 6, 10, 11 etc. |
| 6 | 5, 11, 17 etc. | 1, 2, 3, 4, 6, 7 etc. |
| 7 | 2, 3, 4, 5, 6 etc. | 1, 7, 8, 14, 15 etc. |
| 8 | 3, 5, 7, 11, 13 etc. | 1, 2, 4, 6, 8, 9 etc. |
| 9 | 2, 4, 5, 7, 8, 11 etc. | 1, 3, 6, 9, 10, etc. |
| 10 | 3, 7, 9, 13, 17 etc. | 1, 2, 4, 5, 6, 8 etc. |
| 11 | 2, 3, 4, 5, 6, 7 etc. | 1, 11, 12, 22, 23 etc. |
| 12 | 5, 7, 11, 17, 19 etc. | 1, 2, 3, 4, 6, 8 etc. |
| 13 | 2, 3, 4, 5, 6, 7 etc. | 1, 13, 14, 26 etc. |
| 14 | 3, 5, 9, 11, 13 etc. | 1, 2, 4, 6, 7, 8 etc. |
| 26 | 3, 5, 7, 9, 11, 15 etc. | 1, 2, 4, 6, 8, 10 etc. |
It’s important to give students the opportunity to explore the task and make the mistake of not recording their data. This acts as a valuable lesson for students, when they eventually realise that they can’t remember the results for everything they have already trialled. Furthermore, as students engage in the task, it will become evident to them that they will need to work collaboratively with their peers in order to collect all of the data required in order to identify patterns and make sense of the task.
Therefore, it’s important to leave all students to explore the task on their own for a while. When you see students using creative ways to track their progress or work with each other, you can ask them to share their ideas/strategies with the rest of the lass. If after a while (e.g. 10-15 mins) no one has thought of the need to track their results, you might wish to prompt them by asking which cyphers work/don’t work for each of the alphabets, and how might we track this data to identify patterns? At this point you might even like to draw a table up a table for the students to fill out as a class whilst they collect their data.
Answers
Through exploring this task you may notice that the following conditions don’t work:
- If the cypher and the size of the alphabet share a factor other than one (e.g. cypher of 14x with alphabet Size 8 – share a factor of 2). Therefore in order for the cyper to work, both the cypher and the alhpabet size need to be co-prime.
- If the cypher is 1 – This results in no coding taking place, meaning others can still read the message.
- If the cypher is one more than a multiple of the alhpabet size (e.g cypher 25 for alphabet size 8 – because 3×8+1 = 25). This has the same impact as applying a cypher of 1.
How is this task relevant?
Beyond cryptography becoming an increasingly important area of mathematics as there is an increase in need to protect people’s identity etc. online, there are a number of links to other areas of maths which is task touches on. These include:
- Multiplication & Division with remainders – When applying a cypher of 7x to the letter in the 8th spot, this will result in moving the letter it’s new place in the 56th position. One way to find the 56th position would be to count around the circle 1-by-1, however, students will identify that this is inefficient. Alternatively, if the alphebet contained 10 letters, you could do 56/10 to give you 5 with 6 remainder. This means that you would need to go around the circle 5 times and then count on 6 positions, meaning that it’s the 6th position that you are interested in.
- Co-primes – These are extremely helpful when dealing with fractions. When two denominators are co-prime (e.g. 2/3 +1/5), it means that the lowest common multiple can be found by simply multiplying the denominators together (e.g. 15ths). When the denominators are not co-prime, i.e. share a factor other than one (e.g. 5/6 + 7/9; 6 and 9 share a factor of 3), there will be a lower common multiple other than the product of the two denominators (e.g. 18ths rather than 54ths).
- Algebraic substitution – Applying a cypher is much like substituting into an algebraic equation. For example, you might apply the cypher of 7x, where x is the original position of each letter, or you can take it a step further and apply cyphers such as 7x+3, x^2 etc. This leads to an interesting discussion about how constants affect whether or not a cypher works and why.