Chicken Dinner

  • Chicken Dinner

Chicken Dinner

pdf

Chicken Dinner Game Boards

Size: 5.24 MB
Hits: 622
DownloadPreview
Activity Highlights & Video Explanation

Highlights:

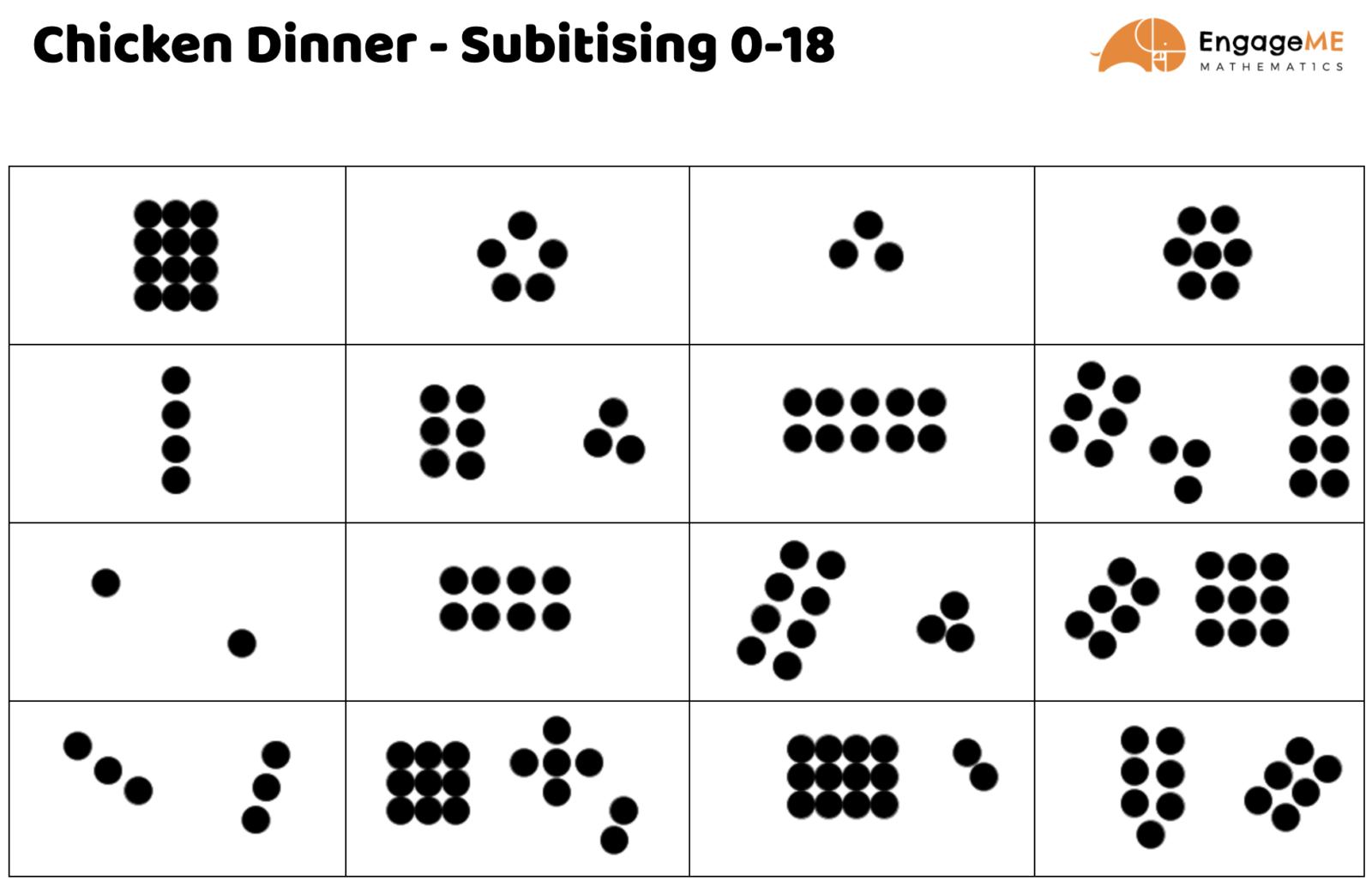
    • Play the Chicken Dinner game with students to develop their part-part-whole knowledge of number.
    • Investigate the different ways numbers from 1-18 can be made
    • Conduct a rich investigation into maximising the chances of winning.

Video Explanation:

Pre-lesson Preparation

Prepare the game boards:

    • Print out the 60 page document (located at the top of the page)
    • Pair each sheet that has dots with another sheet that has a blank table to create 30 different game boards.
    • Laminate the 30 different game boards and store somewhere safe.

Collect equipment:

    • 1x Game board per student
    • Counters or whiteboard markers for marking off spaces on the game board
    • 2x 10-sided dice (numbered 0-9) for teacher
      • Alternatively, Google-search ‘virtual 10-sided dice’
Suggested Learning Goals & Success Criteria
Learning Goals Success Criteria
Subitising by trusting the count
I can:
    • Determine the numbers 1-5 without needing to count dots 1-by-1
    • Determine numbers up to 10 without needing to count dots 1-by-1
    • Determine numbers up to 20 without needing to count dots 1-by-1
Recognising part-part-whole nature of numbers
I can:
    • Determine the different ways the numbers from 1-5 can be made by adding two numbers.
    • Determine the different ways the numbers from 1-10 can be made by adding two numbers.
    • Determine the different ways the numbers from 1-20 can be made by adding two numbers.
Use mathematical reasoning to investigate and problem solve
I can:
    • Identify efficient ways for representing how the numbers from 1-20 can be made by adding two numbers together.
    • Work systematically and use reasoning to identify numbers which are most likely to appear when rolling 2x 10-sided dice (numbered 0-9).
    • Use findings from my mathematical investigation to create a board which has a higher probability of winning and justify my design.

 

Note: You can take this task in many directions and use it to build a range of different social, cognitive, and behavioural skills within your students. The suggestions above are only a few examples of cognitive skills which this task could be used to teach. We recommend you think about the students in your class, their specific learning needs and how this task might be used to address these when determining your learning goals and success criteria for your students.

Prerequisite Skills

This activity requires the following pre-requisit skills:

    • 1:1 correspondence of number
    Engage

    Suggested story hook:

    “When I was younger I use to have a lot of different animals as pets. Some of those animals were Chickens named The Colonel, Clucky and Squaky. My job each night would be to feed the chickens. My chickens loved Peacans! Sometimes I would throw peacans out to them, and without counting the number of peacans I had thrown one-by-one, I would know right away how many I had thrown onto the ground for them to eat. In this game, we’re going to practice this skill. It’s called ‘Chicken Dinner'”
    Main Activity

    Instructions for the game:

      • Each student is given a game board & a set of counters/marker to mark of each number that appears.
      • Roll two 10-sided dice (numbered from 0-9) and add them together.
      • Students then need to idividually find a space on their game board which has the corresponding number of dots in it, and mark it off.
      • The first student to get 4 spaces in a row (horizontal, vertical or diagonal) yells out ‘Winner, winner, chicken dinner!’ and wins the game.

    Pedagogical Recommendations:

      • Once students have located the number on their own game board, encourage them to have a look at the game board of the person next to them to see if they can see the number there. Rather than pointing out the number to their peer, encourage them to say how they can see the number. e.g. I can see a 9 on your game board because I can see a 5 and a 4 or 3 threes etc.
      • Give students the opportunity to find their number, then ask them how they see their number – e.g. if the number was 7, was it a 3 and a 4, was it a 5 and a 2 etc. This highlights the many different parts that can be used to form each number (i.e. part-part-whole).
      • Say the two numbers out aloud and ask a student to add them up for you.
    Extensions

    Taking things further:

      • Play the game many times.
      • Ask students if they notice any numbers which come up more often than others.
      • Ask students to explore whether this comes down purely to chance, or is there something else going on here?
      • Give them time to explore this idea in any way they like.
        • As students do this, roam the room and look for the different strategies students use (i.e. two way tables, ordered list of events etc.)
      • When the moment feels right, select different students who have used novel approaches to share their thinking. If possible, highlight student’s who don’t always contribute.
      • Give students some more time to select one of the methods they saw and use this to investigate the problem further.
      • Get students to then use their new-found knowledge to create their own game board which they believe is most likely to win.
    Summary & Assessment

    Suggested Reflection Prompt:

    It turns out that not all of the original ‘Chicken Dinner’ game boards were created with an equal chance of winning. If your best friend in another class was about to play this game for the first time, what advice would you give them in helping them to select a game board and why?