Beat the Bomb
Beat the Bomb
Activity Highlights & Video Explanation
Highlights:
-
- Hook students into problem solving by engaging them in a story
- Students discover the golden ratio (Phi) for themselves
- An excellent introduction to irrational numbers
Pre-lesson Preparation
Organise equipment
-
- Cut one piece of string for each group.
- Collect 1 peg for each group
- Either print the ‘Beat the Bomb’ handout in colour for students, or project it onto a screen.
Suggested Learning Goals & Success Criteria
| Learning Goals | Success Criteria |
|
To be able to work mathematically
|
I can:
|
| To be able to work collaboratively with peers |
I can:
|
| Identifying and describing irrational numbers |
I can:
|
Note: You can take this task in many directions and use it to build a range of different social, cognitive, and behavioural skills within your students. The suggestions above are only a few examples of the skills which this task could be used to teach. We recommend you think about the students in your class, their specific learning needs and how this task might be used to address these when determining your learning goals and success criteria for your students.
Prerequisite Skills
This activity requires the following pre-requisit skills:
-
- Decimal place value – comparing and ordering
- Interpreting notation relating to lengths
- A developing understanding of ratios
Engage
Suggested intro:
Main Activity
Introduce the main activity:
-
- After showing the randsom note to students, go through anything that they are not sure about as a class. This will likely involve explaining what each of the ratios mean and might require you to demonstrate this for them. Try not to give away too much. The aim is to tell them just enough so that they can make a start for themselves.
- Give students 5 minutes to work on the problem for themselves. This allows each student to enter the group work phase having done some thinking.
- During this phase, wander the room and take not of students who are struggling and the different strategies students are using. This information can then be used to help form groups for the groupwork phase of the lesson.
Group work:
-
- Put students into groups of 3.
- Give each group a measuring tape, one piece of string and a peg. Allow students to use the equipment to assist them with attempting the task.
- As students engage in the task, take note of the different strategies they use. This information can be helpful when forming a plan to discuss the work/solutions as a class.
- Provide assistance and support to groups as required.
- If students finish with one length of string, ask them to attempt it with another length and see what they notice.
Class discussion:
-
- As you roam the class and take note of how students attempted the task, you will notice that they will likely use different strategies to solve it. Begin the class discussion by asking students with the least complex strategy to share, and then invite other groups up to share their strategies in order of increasing complexity.
- As students share their strategies, get them to compare how the different strategies relate to each other and identify the strengths and weaknesses of each strategy.
- Conclude the lesson by looking at the similarites in relation to the ratios each group discovered, despite having strings of different lengths.
Extensions
Taking things further:
-
-
Get students to research the golden ratio and put together a 2minute explanation about what they find. Ask them to share this with the class at the end of the lesson.
-
Summary & Assessment
Suggested Reflection Prompt:
Get students to answer the following prompts:
- Is it possible to cut the wire in exactly the right place? Explain your thinking…
- Describe the difference between rational and irrational numbers.
- What strategy did you find most helpful for solving the ‘Beat the Bomb’ task? If you were to do this task again, how might you go about solving it differently?
Spoilers: Helpful Hints & Answers
Helpful Hints
Students may choose to attempt the problem in many different ways. Here are some ways which might be helpful:
- Using a piece of string and a peg can assist students initially to keep track of their lengths and results.
- Students may also choose to record their results in a table.
- Alternatively, students might choose to use a spreadsheet to perform their calculations e.g.
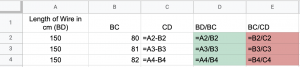
- Albeit unlikely for students in this age range, this problem can also be solved algebraically. Here’s a video of one of our favourites, Matt Parker demonstrating this.
Answers
As you and your students explore this task, you will discover that no matter what lengths you try, you can always become more and more accurate, meaning that there is no solution, and unfortunately for everyone, the bomb will go off!! KABOOM!!
However, as you explore the task, you will also notice that it doesn’t matter how long the original piece of wire is, the ratio will always approach 1.618… This is known as the golden ratio, an irrational number that is highly worth exploring with your students.
How is this task relevant?
Beyond sending your students into a manic frenzy as they leave the classroom at the end of the lesson pretending that a bomb is about to explode, this lesson leads to two really nice insights. These are:
- A conceptual understanding of irrational numbers. Through experiencing a number that requires a never ending process, students will be primed to learn about irrational numbers and how they differ to rational numbers.
- The discovery of the Golden Ratio. It has been suggested that this special ratio can be found in many different walks of life. From logos, to photography, to graphic design, to nature and even what makes people physically attractive. Despite many mathematicians claiming that it’s significance is overrated, there are many people who believe that this ratio has special properties which are hidden almost everywhere.

